In the case of a reflection, if all rays intersect at a point as if it were a real image, it’s called a virtual image. In the case where light actually does appear from some point on which rays appear to converge, it’s considered a real image.

To define a few things:

the optical axis is a line about which a mirror is symmetric
the centre of curvature C is the centre of a circle
the radius of curvature R is the radius of a circle

In the case of a concave mirror, all rays parallel to the optical axis intersect at the same point, with distance from intersection point being defined by the following: $a = R / (2 cos (θ))$ For small angles, $A$ is approximately $R /2$ .

For convex mirrors, the geometry is similar but rays parallel to the axis reflect as if they come from the focal point, on the opposite side of the mirror.

That point of note in both cases is called the focal point, noted $f$ . Arbitrarily, $f$ is defined positive for concave mirrors, and defined negative for convex mirrors. The sign for the radius of curvature follows that of the focal point.

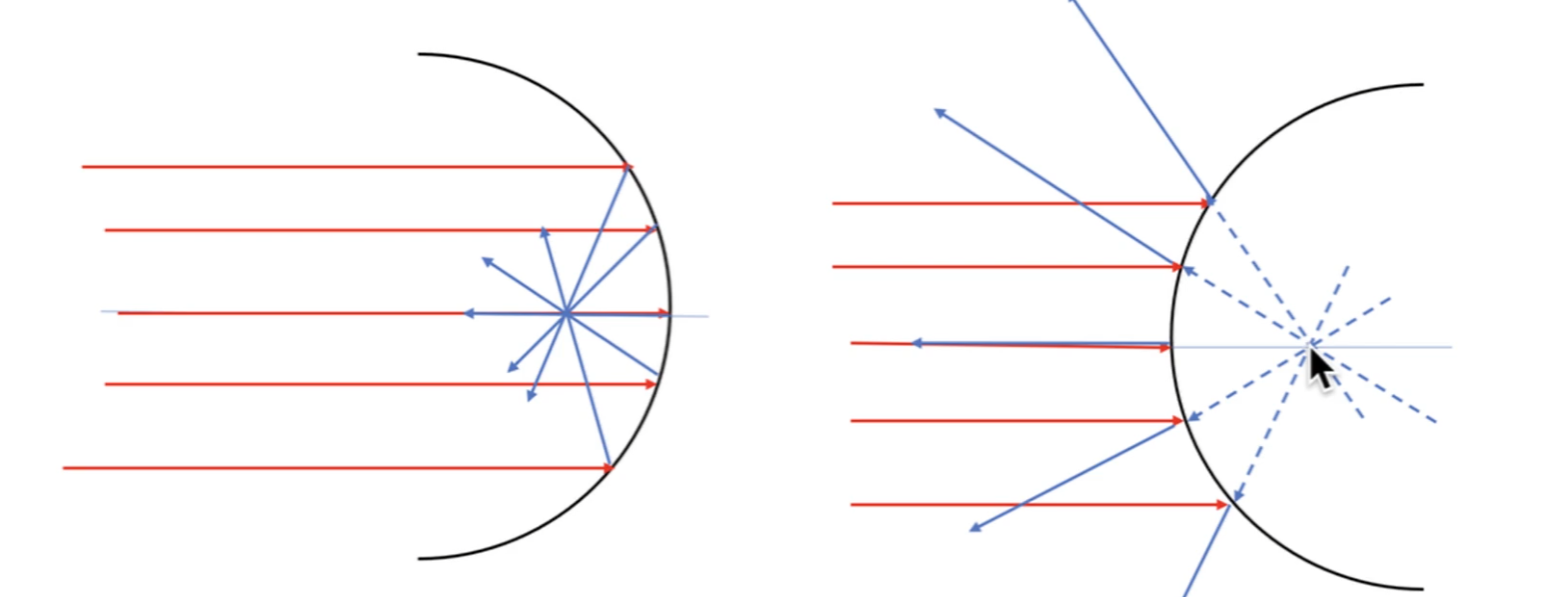
Rays going through the centre of curvature are reflected back the same way they came, and rays hitting the mirrors on the axis are reflected symmetrically about the axis(as expected).

Table

Direction of Ray	Concave Mirror	Convex Mirror
Parallel to axis	Passes through focal point	Appears to come from focal point
Directed toward center of curvature	Reflects back along original path	Reflects back along original path
Directed to where optical axis meets mirror	Reflected symmetrically	Reflected symmetrically

Formulaic Definitions

$d_{o}$ is an object’s distance to a mirror
$d_{i}$ is the distance of the image from the mirror The ratio of the image to object heights is given simply by $h_{i} / h_{o} = d_{i} / d_{o}$ , the relationship between $d_{o}$ and $d_{i}$ is given by $\frac{1}{d _{o}} + \frac{1}{d _{i}} = \frac{1}{f}$ , and the magnification is given by $m = - \frac{d _{i}}{d _{o}}$ In order to properly apply these, a few mathematical assumptions must be made:
The distance to the object is positive
The focal length of concave mirrors is positive
The focal length of convex mirrors is negative
The distance to a real image is positive
The distance to a virtual image is negative When the ratio of $d_{i} / d_{o}$ is negative, $m$ is positive, and the image is upright. When the ratio of $d_{i} / d_{o}$ is positive, $m$ is negative, and the image is inverted.

physics light

Triaksha's Notes 🍀

Explorer

Images, Focal point

Table

Formulaic Definitions

Graph View