Beam Structures

Beams are structural members designed to support loads applied perpendicular to their axes.

Method of Sections

The method of sections is used to find forces acting within a member to make sure a member can resist the loads applied to it. Typical internal loads include:

• Normal force $N_B$ , acting perpendicular to the cut cross section
• Shear force $V_B$ , acting tangent to the cross section
• Bending moment $M_B$ , preventing relative rotation between sections

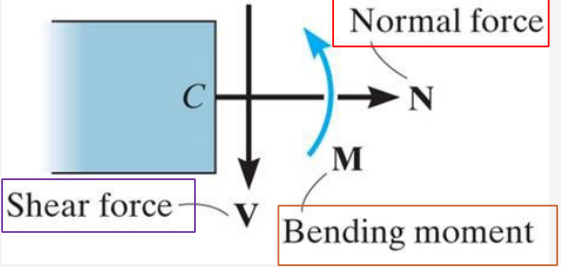
To determine internal force values, apply the equations of equilibrium in the case that the beam is static.

In terms of structure for a problem:

1. Determine support reactions
2. Cut the beam at the point to examine
3. Draw FBD of one of the halves, including internal forces acting at the point
4. Solve for unknowns using equations of equilibrium

For sign convention,

• $N_B$ is positive if it creates tension
• $V_B$ is positive if it causes the beam to rotate clockwise
• $M_B$ is positive if the beam bends upwards in a concave manner

3D

Internal forces in 3D:

• Normal force acts perpendicular to cross section
• Shear force acts tangent to cut cross section
• Bending moment components prevent relative rotation between the two segments
• Torsional moment is the twisting moment

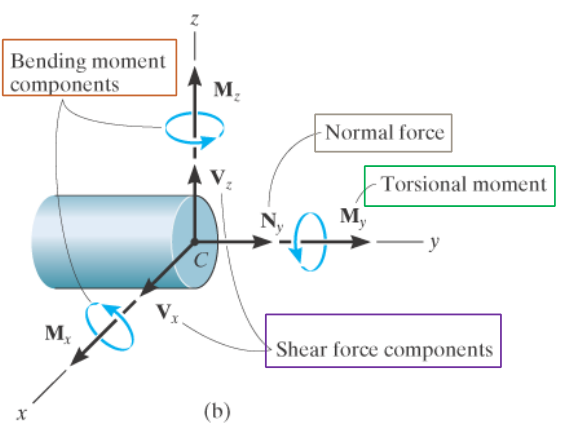
• Determine support reactions of entire beam, if needed

2. Take an imaginary cut at the place where you need to determine the internal forces
3. Draw the FBD of each section including the internal forces (N, V, M) at the cut cross section using the established sign convention
4. Select the resulting section or piece that will be easier to analyze
5. Apply the Equations of Equilibrium
   1. •Moments should be summed at the cut section to eliminate the N and V
   2. If the solution yields a negative scalar, the sense is opposite to that drawn on the FBD

physics statics